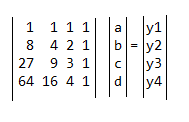.1…2…3…4…5…6.
.8…14…22…32…44…58
to wynika z tego wzoru: …->…x*x +3x +4
.1…2…3…4…5…6.
.8…14…23…35…50…68
a to; …->…???
Czy jest jakaś tabela w Internecie,
żeby wpisać te dane i otrzymać wzór?
Albo inny sposób.
Zależy na jakim poziomie zaawansowania chcesz to rozpracowywać. Najprościej jest policzyć różnicę kolejnych wartości w danym wierszu aż do takiego wiersza, gdzie różnica wyniesie 0:
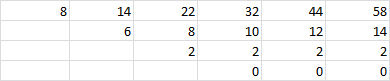
i wtedy wiedząc, ile masz tych pośrednich wierszy, takiego stopnia masz wielomian (tu 2 wiersze, czyli y=ax^2+bx+c. Podstawiasz za x oraz y kolejne pary wartości i rozwiązujesz układ równań (tu z 3 niewiadomymi: a, b i c).
Analogicznie dla drugiego przykładu masz:
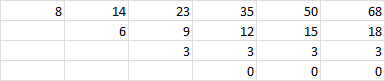
Czyli też wielomian 2 stopnia. I teraz:
dla x=1: a+b+c=8
dla x=2: 4a+2b+c=14
dla x=3: 9a+3b+c=23
otrzymujesz
a=1.5
b=1.5
c=5
czyli y=1.5x^2+1.5x+5
PS. x^2 = x*x
Rozumowanie jak najbardziej poprawne, ale nie jest to jedyny sposób dojścia do rozwiązania problemu.
Nie biorąc nawet pod uwagę pierwszego przykładu można np. zauważyć, że różnice między kolejnymi wyrazami ciągu, to:
6,9,12,15,18 ale 6=23 9=33 12=43 15=53 18=6 * 3 a pierwszy wyraz 8=5+1 * 3
czyli dowolny wyraz tego ciągu można przedstawić jako sumę: y=5+13+23+…+ x*3 gdzie x to numer ostatniego wyrazu w ciągu. Po wyłączeniu liczby 3 przed nawias otrzymamy: y=5+(1+2+…x)3
Wyrażenie w nawiasie to suma wyrazów ciągu arytmetycznego:1+2+…+x=x(1+x)/2 czyli
y=5+3x(1+x)/2=1,5x^2+1,5x+5 , a więc jest to wielomian stopnia drugiego.
Jeżeli przyjmiemy, że kolejne wyrazy takich ciągów są wartościami wielomianów stopnia drugiego, to znajdowanie tych wielomianów rzeczywiście można sprowadzić do rozwiązania układ równań jak w poniższym przykładzie i czynność taką można zautomatyzować, aby liczył to komputer:
a+b+c=8
4a+2b+c=14
9a+3b+c=22
gdzie liczby 8, 14 ,22 można zastąpić innymi.
Dzięki za tabelę.
Z tego wynika, że:
po zmianie tabeli: od x = 0
0…1…2…3…4…5…6
5…8…14…23…35…50…68
,
…3…6…9…12…15…18
…3…3…3…3…3
obliczenia wykonujemy na liczbach początkowych wierszy.
jeśli w 2-m wierszu jest 3, to dzielimy przez 2 i otrzymujemy:…a = 1,5
jeśli od pierwszego wiersza (3) odejmiemy te 1,5 otrzymamy:…b = 1,5
i dla wartości x = 0…->…y = 5 … więc:… c = 5
Czy dobrze kombinuję?
A można obliczyć a, b i c przy pomocy prostego skryptu np. VBS?
Oczywiście, że można. W tym działającym programiku masz napisane rozwiązanie tego układu równań.
zagadka.zip (7,9 KB)
Nie wiadomo w czym to pisane, ale to nie będzie skrypt.
Już to rozwiązałem.
Y1 = 8
Y2 = 14
Y3 = 22
c = 3 * Y1 - 3 * Y2 + Y3
b = 2 * Y1 - 0.5 * Y2 - 1.5 * c
a = Y1 - b - c
po redukcji to samo jak w zagadce
a = 0.5 * Y1 - Y2 + 0.5 * Y3
b = -2.5 * Y1 + 4 * Y2 - 1.5 * Y3
c = 3 * Y1 - 3 * Y2 + Y3
Dzięki za pomoc.
Wielomian 2 stopnia z trzema niewiadomymi
ax^2 + bx + c
rozwiązanie:
a = 0.5 * Y1 - Y2 + 0.5 * Y3
b = -2.5 * Y1 + 4 * Y2 - 1.5 * Y3
c = 3 * Y1 - 3 * Y2 + Y3
…
Wielomian 3 stopnia z czterema niewiadomymi
ax^3 + bx^2 + c*x + d
rozwiązanie:
a =
b =
c =
d=
Jak wygląda to rozwiązanie?
ax^3+bx^2+cx+d
x=1 to a+b+c+d=y1
x=2 to 8a+4b+2c+d=y2
x=3 to 27a+9b+3c+d=y3
x=4 to 64a+16b+4c+d=y4
Zapisujemy ten układ równań w postaci macierzowej i rozwiązujemy go.
Poszukaj i poczytaj: Rownania macierzowe