Taki mi sie rzucił temat na ruszt.
Zastanowiło mnie połączenie ciągu Fibonacciego ze zbiorem liczb pierwszych.
Uznałem, że przeprowadzę eksperyment i wyrysuję programowo spiralę, a następnie naniosę liczby Fibonacciego oraz liczby Pierwsze.
Gdyby była już taka spirala komuś znana to całkiem dobrze się składa, bo to co ja zauważam może jest wiadome, ale nie było dla mnie jeszcze przed eksperymentem.
Otóż liczby pierwsze na spirali występują w bardzo losowy sposób, to jest pewne.
Jednak jest to układ współgrający z liczbami Ciągu Fibonacciego. Jak? O tym za chwilę.
Przybywa ich pomiedzy kolejnymi wyrazami ciągu Fibonacciego, to jest pewne.
Z obserwacji wynika też taka mało trywialna sprawa, że:
Suma liczb pierwszych na spirali pomiędzy kolejnymi wyrazami ciągu Fibonacciego podzielona przez ilość liczb pierwszych, a następnie podzielona przez większą liczbę Fibonacciego daje w przybliżeniu połowę Złotej liczby Phi.
Wyjątkiem jest początek spirali, gdzie wartości są równe 1, dla liczb 2,3,5.
Czyli zbiór jest w pewnym sensie związany ze złotą spiralą w ten sposób. Czy może to zbyt naciągany wniosek?
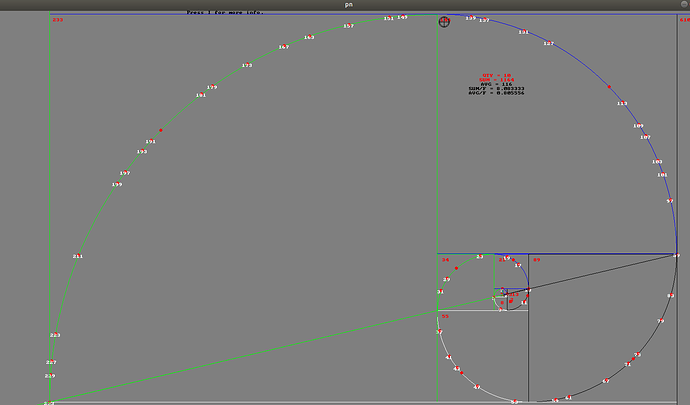
Proszę zarkąć na obrazek okna aplikacji, która narysowała spiralę i nanosiła liczby Pierwsze. (nie wiem czy da się skalować, bo przy pomniejszonych raczej nie bedzie za wiele widać).
Opis tego, co widzisz na ekranie.
Liczby pierwsze są w kolorze białym.
QTY - ilość liczb pierwszych między kolejnymi liczbami ciągu Fibonacciego, tj. w danym kwadracie.
SUM - suma liczb pierwszych między kolejnymi liczbami Fibonacciego.
AVG - średnia obliczona poprzez podzielenie sumy przez ilość, tj. SUM / QTY.
SUM / F - suma liczb pierwszych podzielona przez liczbę Fibonacciego.
AVG / F - pokazuje średnią liczb pierwszych w danym polu kwadratowym, podzieloną przez większą liczbę Fibonacciego.
Zauważ, że. Wygląda na to, że zawsze jest to przybliżenie równe połowie Złotej Liczby Phi / 2 ≈ 0,80 … z wyjątkiem pierwszych trzech liczb (2,3,5), które są równe liczbom Fibonacciego, a dobre przybliżenie wzrasta wraz ze wzrostem wartości.
Chciałbyś zrobić eksperyment i sprawdzić? Ja zrobiłem dla dalszych wartości… i to przypuszczenie się potwierdza. Napisz w komentarzu a udostępnię Ci małą aplikację do wyliczenia tego w wierszu poleceń dla Windows. Chciałbys programik do rysowania spirali, w którym stworzyłem te rysunki? Też moge udostępnić.
Wyniki eksperymentu są zadziwiająco dokładne, ale ich obliczenie zajmuje chwilę mojemu komputerowi.
Podam formułę matematyczną, która wynika z tego powyższego twierdzenia.
Oto jej postać:
SP=1/2∗Phi
SP=(((P1+P2+…+Pn))/QP)/GF
Gdzie:
SF<Pn<=GF
P1,P2,Pn - są to liczby pierwsze
SF - mniejsza wartość ciągu Fibonacciego (dolna granica zbioru)
GF - wieksza wartość ciągu Fibonacciego (górna granica zbioru)
SP - suma liczb pierwszych w podzbiorze
QP - ilość liczb pierwszych w podzbiorze
Phi - Złota Liczba Phi 1.618…
Przykładowy listing obliczeń z programu …
________________________________________________________________________
THAT APP IS CALCULATING THE PRIME NUMBERS SUBSETS
BETWEEN FIBONACCI AND FINDING APPROXIMATION____
TO THE GOLDEN NUMBER_PHI._______________________
Author: Sylwester B aka Sylvi91_______________
Fib(1) = 1 - Fib(2) = 1
Primes list:
Primes: Sum = 0 Qty = 0 Avg = 0.000000
Approximation to the The Golden Number Phi = 0.000000
Fib(2) = 1 - Fib(3) = 2
Primes list:
2
Primes: Sum = 2 Qty = 1 Avg = 2.000000
Approximation to the The Golden Number Phi = 2.000000
Fib(3) = 2 - Fib(4) = 3
Primes list:
3
Primes: Sum = 3 Qty = 1 Avg = 3.000000
Approximation to the The Golden Number Phi = 2.000000
Fib(4) = 3 - Fib(5) = 5
Primes list:
5
Primes: Sum = 5 Qty = 1 Avg = 5.000000
Approximation to the The Golden Number Phi = 2.000000
Fib(5) = 5 - Fib(6) = 8
Primes list:
7
Primes: Sum = 7 Qty = 1 Avg = 7.000000
Approximation to the The Golden Number Phi = 1.750000
Fib(6) = 8 - Fib(7) = 13
Primes list:
11 13
Primes: Sum = 24 Qty = 2 Avg = 12.000000
Approximation to the The Golden Number Phi = 1.846154
Fib(7) = 13 - Fib(8) = 21
Primes list:
17 19
Primes: Sum = 36 Qty = 2 Avg = 18.000000
Approximation to the The Golden Number Phi = 1.714286
Fib(8) = 21 - Fib(9) = 34
Primes list:
23 29 31
Primes: Sum = 83 Qty = 3 Avg = 27.000000
Approximation to the The Golden Number Phi = 1.588235
Fib(9) = 34 - Fib(10) = 55
Primes list:
37 41 43 47 53
Primes: Sum = 221 Qty = 5 Avg = 44.000000
Approximation to the The Golden Number Phi = 1.600000
Fib(10) = 55 - Fib(11) = 89
Primes list:
59 61 67 71 73 79 83 89
Primes: Sum = 582 Qty = 8 Avg = 72.000000
Approximation to the The Golden Number Phi = 1.617978
Fib(11) = 89 - Fib(12) = 144
Primes list:
97 101 103 107 109 113 127 131 137 139
Primes: Sum = 1164 Qty = 10 Avg = 116.000000
Approximation to the The Golden Number Phi = 1.611111
Fib(12) = 144 - Fib(13) = 233
Primes list:
149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233
Primes: Sum = 3223 Qty = 17 Avg = 189.000000
Approximation to the The Golden Number Phi = 1.622318
Fib(13) = 233 - Fib(14) = 377
Primes list:
239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373
Primes: Sum = 6989 Qty = 23 Avg = 303.000000
Approximation to the The Golden Number Phi = 1.607427
Fib(14) = 377 - Fib(15) = 610
Primes list:
379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607
Primes: Sum = 18165 Qty = 37 Avg = 490.000000
Approximation to the The Golden Number Phi = 1.606557
… i dalej bez listowania liczb pierwszych, a tylko z wyliczeniem sumy oraz ilości i średniej i przyblizonej wartosci liczby Złotej.
Fib(15) = 610 - Fib(16) = 987
Primes: Sum = 43635 Qty = 55 Avg = 793.000000
Approximation to the The Golden Number Phi = 1.606890
Fib(16) = 987 - Fib(17) = 1597
Primes: Sum = 109567 Qty = 85 Avg = 1289.000000
Approximation to the The Golden Number Phi = 1.614277
Fib(19) = 4181 - Fib(20) = 6765
Primes: Sum = 1624217 Qty = 297 Avg = 5468.000000
Approximation to the The Golden Number Phi = 1.616556
Fib(27) = 196418 - Fib(28) = 31781
Primes: Sum = 2499980948 Qty = 9738 Avg = 256724.000000
Approximation to the The Golden Number Phi = 1.615577
…
Aktualnie ustawiłem aplikację do wyciągania Złotej Liczby ze zbiorów liczb pierwszych dla górnego przedziału do 44 liczby ciągu Fibonacciego, która ma wartość 701408733… komputer już oblicza którą godzinę i jeszcze pewnie sporo mu zostało do końca. Ale to starej generacji procek w środku.
Co do algorytmu to może nie jest najszybszy, bo stosuję tablicę liczb pierwszych wyznaczoną metodą Sita Eratostenesa, a więc starożytny już algorytm… który mimo to sprawdza się w dobie komputerów.
Co do powiązania zbioru liczb pierwszych ze złotą spiralą i złotą liczbą to niewiele słyszałem do tej pory, a Wy znacie taką formułę lub słyszeliście o tym?